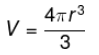Ao longa da história, surgiu a necessidade de realizar a medida de volume de determinados objetos. Como consequência, surgiram as unidades de medidas de volume. Hoje utilizamos como padrão as medidas adotadas pelo Sistema Internacional de Unidades, que considera o metro cúbico ( m³) a unidade-padrão para medida de volume.
Além do metro cúbico, existem seus múltiplos (decâmetro cúbico, hectômetro cúbico e quilômetro cúbico) e submúltiplos (decímetro cúbico, centímetro cúbico e milímetro cúbico). É importante relacionar as medidas de volume com as medidas de capacidade, que é medida em litro (1 m³ corresponde a 1.000 litros). Ao longo da história, existiram outras medidas de volume, como a polegada cúbica, o pé cúbico, a jarda cúbica e a milha cúbica.

Quais são as medidas de volume?
Atualmente, pelo Sistema Internacional de Unidades, a unidade-padrão de volume é o metro cúbico. Utilizamos uma unidade cúbica porque o volume é tridimensional, ou seja, envolve comprimento, largura e altura.
A partir do metro cúbico, temos as unidades conhecidas como múltiplos. Utilizamos essas unidades para realizar medição de objetos que ocupam um espaço muito grande. Os múltiplos do metro cúbico são:
decâmetro cúbico (dam³);
hectometro cúbico (hm³);
quilômetro cúbico (km³).
Existem também os submúltiplos do metro cúbico, que são unidades de medida utilizadas para medir volumes menores. Os submúltiplos do metro cúbico são:
decímetro cúbico (dm³);
centímetro cúbico (cm³);
milímetro cúbico (mm³).
Conversão de unidades
Conhecendo os múltiplos e submúltiplos de unidade-padrão de volume, podemos realizar a conversão de uma unidade de medida para outra. Para isso, devemos considerar a tabela a seguir.
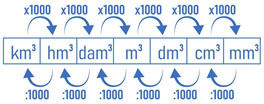
Perceba que, para transformar uma unidade maior, que está à esquerda, para uma unidade menor, que está à direita, para cada unidade de medida, vamos multiplicar o valor por 1000.
Exemplo:
2 km³ → dam³
Note que são duas unidades de medida, logo vamos multiplicar o valor por 1000 para transformar de km³ para hm³ e, depois, por 1000 de novo para transformar de hm³ para dam³. Isso também pode ser feito de forma direta, ou seja, multiplicando o valor por 1 000 000.
2 x 1 000 000 = 2 000 000 dam³
Agora, para transformar uma unidade menor para uma unidade maior, ou seja, ir da direita para a esquerda, para cada unidade de medida, vamos dividir por 1000.
Exemplo:
15 000 000 mm³ → m³
De mm³ para m³, há 3 unidades, logo vamos dividir por 1000 para cada unidade, ou seja, dividiremos por 1 000 000 000.
15 000 000 : 1 000 000 000 = 0,015 m³
Medidas de volume e medidas de capacidade
Essas medidas muitas vezes se misturam, pois geralmente medimos o volume de objetos para saber a sua capacidade. Acontece que a capacidade tem como unidade de medida padrão o litro e um dos interesses na medição do volume é descobrir qual a quantidade de litros que posso colocar naquele recipiente. Logo, tanto para provas e exames como para a aplicação dessas medidas no dia a dia, é importante saber a relação entre metros cúbicos e litros.
1m³ = 1 000l
1dm³ = 1l
1cm³ = 1ml
Assim sendo, para saber a capacidade de um objeto com volume conhecido e medido em metros cúbicos, basta multiplicar o volume por 1000.
Como calcular o volume de sólidos geométricos?
Encontrar o volume de um sólido geométrico é fundamental para várias atividades do nosso cotidiano, por exemplo, para saber a capacidade de um galpão, para saber o espaço ocupado por um determinado móvel da nossa casa. Calculamos o volume utilizando fórmulas específicas para cada um dos sólidos geométricos. Vejamos agora as fórmulas de volume dos principais sólidos geométricos da geometria espacial.
Volume do prisma
Começando pelo prisma, um dos sólidos mais comuns no cotidiano. O prisma é todo sólido geométrico que possui duas bases iguais e faces laterais formadas por paralelepípedos, por exemplo, caixas de sapato, prédios, entre outros objetos.
Para calcular o volume do prisma, é necessário conhecer a área da base, que pode ser formada por qualquer polígono. O volume do prisma é calculado pelo produto entre a área da base e a altura do prisma.
Vprismas = Ab · h
Ab = área da base
h = altura do prisma
Existem dois casos particulares de prisma bastante recorrentes que são o cubo e o paralelepípedo retangular.
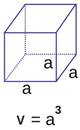
Volume do Cubo
Começando pelo cubo, sabemos que ele possui todas as arestas congruentes. Então, para calcular o volume do cubo, sabemos que a área do quadrado é igual ao quadrado da aresta. Para calcular o volume, multiplicamos pela altura, que, no caso do cubo, também é igual à medida da aresta. Assim, o volume do cubo é dado por:
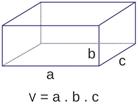
Volume do Paralelepípedo
O volume do paralelepípedo retângulo pode ser encontrado quando multiplicamos as suas três dimensões:
Volume das Pirâmides
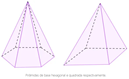
A pirâmide é o sólido geométrico que possui a base formada por um polígono e as faces laterias formadas por um triângulo, ligando os vértices da base a um ponto fora da base conhecido como vértice da pirâmide. Assim como o prisma, a pirâmide também pode possuir diferentes bases.
Para calcular o volume da pirâmide, é necessário calcular a área da base. O volume da pirâmide é dado pela fórmula:
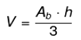
Volume do Cilindro
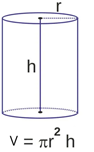
O cilindro é o sólido geométrico que possui duas bases circulares de mesmo raio. Classificado como um corpo redondo devido a sua forma arredondada, esse sólido geométrico é bastante recorrente em embalagens como as de achocolatado e de outros produtos.
Para calcular o volume de um cilindro, precisamos apenas da medida do seu raio e da sua altura:
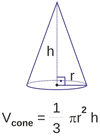
Volume do Cone
O cone também é classificado como um corpo redondo. Ele possui a base formada por um círculo e um vértice. Para calcular o volume do cone, também é necessário conhecer a sua altura e o raio de sua base:
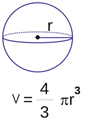
Volume da Esfera
A esfera é também um formato comum no dia a dia, como as bolas que utilizamos para praticar certos esportes, além de ser um formato comum na natureza. Para calcular o volume da esfera, é necessário conhecer somente o seu raio:
Resumo sobre o volume dos sólidos geométricos
Cada sólido geométrico possui uma fórmula diferente para o cálculo do seu volume. O volume de um sólido é medido em unidades cúbicas, como metros cúbicos, centímetros cúbicos, entre outras.
Fórmula para calcular o volume do prisma:
V = Ab · h
Fórmula para calcular o volume da pirâmide:
![]()
Fórmula para calcular o volume de um cilindro:
V = π r² · h
Fórmula para calcular o volume de um cone:
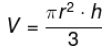
Fórmula para calcular o volume da esfera: