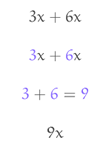
Simplificar uma expressão algébrica é escrevê-la da maneira mais curta possível.

A simplificação de uma expressão algébrica ocorre pelas operações da aritmética adição e subtração. Consiste em pegar os termos semelhantes e somar ou subtrair para tornar a expressão mais simples e fácil de operar.

A simplificação acontece conservando as variáveis (parte literal) e somando ou subtraindo os coeficientes (números).

Você também deve aprender as regras que você verá abaixo.

Adição e subtração de variáveis

Você só pode adicionar ou subtrair variáveis iguais, isto é, representadas com a mesma letra. Para isso, adicione ou subtraia seus coeficientes e mantenha a variável. Por exemplo:

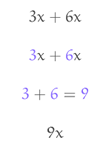
Multiplicação e divisão de variáveis

No caso dessas operações, você pode multiplicar ou dividir variáveis diferentes ou representadas com letras diferentes. Para isso, multiplique ou divida seus coeficientes e mantenha as variáveis. Por exemplo:

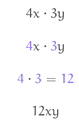
Propriedade distributiva

A propriedade distributiva afirma que um coeficiente multiplica cada um dos termos dentro de um parêntese. Veja como esta propriedade é aplicada abaixo:

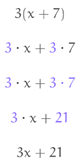
Agora que você conhece essas regras, veja um último exemplo para aplicar tudo o que sabe. Simplifique a seguinte expressão:

O primeiro passo é resolver o parêntese com o coeficiente 4   :

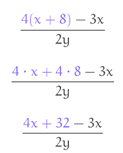
Agora podemos adicionar variáveis iguais:

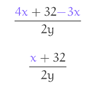
Não é possível simplificar ainda mais, então nossa expressão ficará assim:

Fonte: https://edu.gcfglobal.org em 25/06/2023

Índice --- Exercício 11